「無限」と聞いて何を思い浮かべるだろうか。
終わりのない数列、宇宙の広がり、あるいは哲学的な抽象。
しかし、無限にも“大小”があると聞いたらどうだろう。
直感に反するこの事実を、あるホテルの物語が鮮やかに描き出す。
今回は、数学が紡ぐ思考実験「ヒルベルトのホテル」を通じて、無限の奥深さに触れてみたい。

無限にも「大小」があるという逆説

無限の中に、より大きな無限が存在するという直感に反する事実。
きっかけは、偶然目にした4年前のYouTube動画。
テーマは「無限のサイズ」という数学的な迷宮。

ヒルベルトの無限ホテル

舞台は、無限に部屋を持つ架空のホテル。
一つの部屋に一名の宿泊客しか泊まれないとする。
各部屋には自然数が割り振られ、すべての部屋に宿泊客が滞在中。
つまり、無限の部屋に無限の宿泊者。
ここから始まる思考実験。

🏨 レベル１：新しい宿泊者の到着

すでに満室のはずのホテルに、新たな宿泊者が到着。
無限の部屋に無限の客。満室と断言できるか。
もちろん、答えはNO。無限には「余地」がある。

解法：隣室への移動

全宿泊者に対し、部屋番号を1つずつずらすようアナウンス。
部屋1の客は部屋2へ、部屋2の客は部屋3へ。
こうして部屋1が空き、新しい客を迎え入れる余地が誕生。
有限の人数であれば、何人でも対応可能。
例えば100人なら、全員を部屋番号＋100へ移動させればよい。

有限の追加に対応する無限の柔軟性

• 部屋番号のシフトで新規客を収容
• 有限人数なら何人でも対応可能

🚌 レベル2：無限の団体客の到着

次に到着したのは、無限の人数を乗せたバス。
無限の客をどう収容するか。

解法：偶数部屋への再配置

既存の宿泊者を、部屋番号の2倍の部屋へ移動。
部屋1 → 部屋2、部屋2 → 部屋4、部屋3 → 部屋6。
奇数番号の部屋がすべて空室となり、そこに新たな無限の客を収容。
奇数部屋もまた、無限の数。無限の中に、さらに無限の余地。

偶数倍の再配置で奇数部屋を確保

• 無限の奇数部屋という“余白”の活用
• 無限の中に、さらに無限の空き

🧮 レベル3：無限台のバス × 無限人

さらにスケールアップ。
無限台のバス、それぞれに無限の乗客。
無限 × 無限の到着。

解法：座標とジグザグ列挙

バス番号を縦軸、座席番号を横軸とする座標系を導入。
各乗客に「Bus1Seat1」「Bus2Seat3」などの識別子を付与。

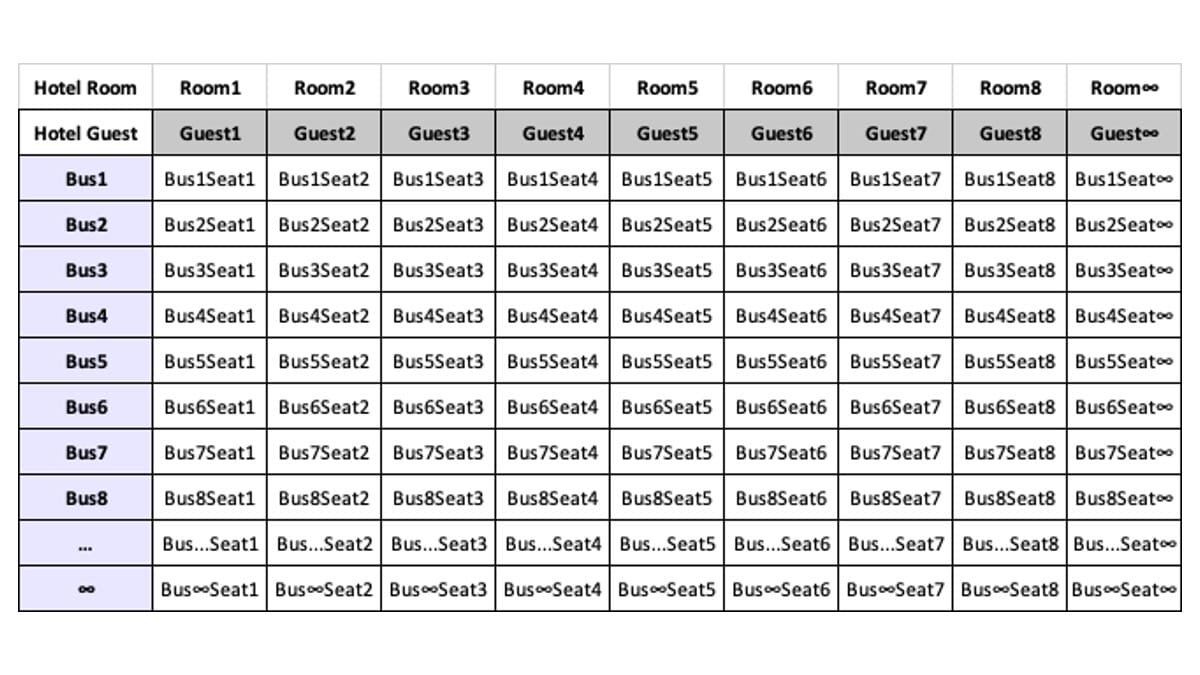
この無限の集合を一列に並べるため、Z字型に走る線を引く。
この線がすべての座標を一度ずつ通過するよう設計。

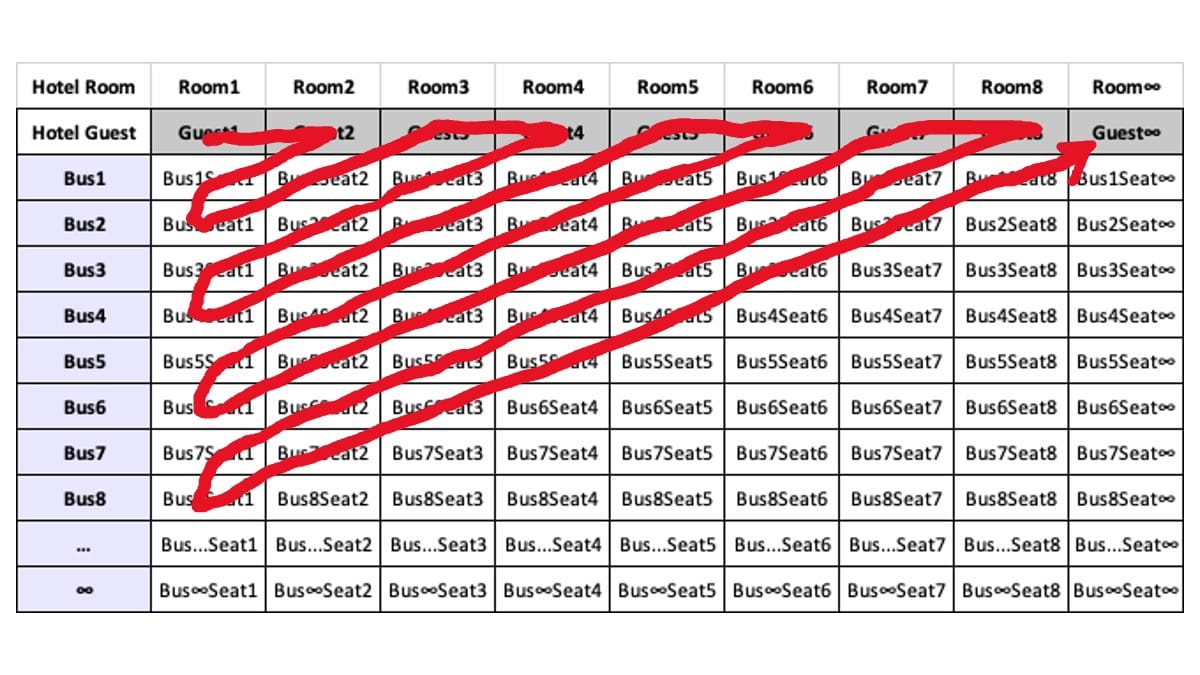
線をまっすぐに伸ばせば、すべての乗客に一意の番号を割り当て可能。

無限の部屋に、無限の乗客を収容。思考実験の勝利。

座標とZ字列挙による一意の割り当て

• バス番号 × 座席番号の座標化
• Z字型の走査で一列に並べる
• 無限の整理術の美しさ

🔤レベル4：名前だけで識別される無限の客

最後の挑戦。
座席のないバスに乗っているのは、名前だけで識別される乗客たち。
名前は、AとBの文字による無限の並び。
例：「ABABABBBABAABA…」「ABBAAAAAAAAAA…」
このバスには、AとBの無限の組み合わせが存在。

⛔️ 問題の発生

この集合は、前の方法では収容不可能。
Excelで名前を並べ、順に文字を反転させていく操作を想定。
1人目の1文字目をA→B、2人目の2文字目をB→A…と続ける。
この操作によって、必ず「どの名前にも一致しない名前」が生成される。
つまり、どの部屋にも割り当てられない客の存在。
ここで初めて、無限の限界に直面。

実数の無限と自然数の無限の違い

• AとBの無限の並びによる識別
• どの名前にも一致しない名前の存在
• 無限の中にも“収容不可能”な集合

🧠 結論：無限にも階層があるという事実

自然数の無限よりも、実数の無限のほうが「大きい」こと。
集合論が示す、無限の中のヒエラルキー。
無限の奥深さと、直感を裏切る論理の美しさ。

Youtubeの動画（英語）：

🇨🇳Chinese/ 中文

无穷大∞的悖论

有一些“无穷大”比另一些“无穷大”要大？“无穷大”也分大小？

最近偶然看到一个4年前的Youtube视频，科普了这个迷人的概念。

无限酒店

假设你是一家酒店的大堂经理。这个酒店有无穷大间房间，每个房间有一个自然数号码，每个房间里面有一个房客，因此有无穷大名房客住在无穷大间房间里。

思想实验从这里开始。

🕹️【第一关】

酒店迎来了一位新客人，他需要一间房间。但是你已经有无穷大的房客住在无穷大间房间里。你能说你满员了吗？似乎不对。因为你有无穷大间房间，数量是无穷尽的。

⬇️ 解决方法：

你拿起麦克风，通知所有房客说，现在每个人收拾行李搬到隔壁房间去。于是房间1的客人帮到房间2，房间2的客人半岛房间3，以此类推。
于是新房客可以入住房间1。

ℹ️ 使用这个方法，不论你来了多少名新房客，只要是有限数量的，你都可以使用这个方法。比如你需要安置100个新房客，只要要求所有房客移动到房间号+100的房间里即可。

🕹️【第二关】

假设你迎来了团体客户。一辆巴士上坐着无穷大数量的人，这些人要入住酒店。怎么办呢？

⬇️ 解决方法：

你要求所有现有房客入住到现在房间号2倍的房间去。房间1的客人搬去房间2，房间2的客人搬去房间4，房间3的客人搬去房间6，以此类推。这样一来所有奇数号码的房间被空出来，而你有无穷大间奇数号码的房间，可以入住无穷大名新房客。问题解决。

🕹️ 【第三关】

酒店迎来更大规模的团体客户。有无穷大辆巴士，每辆巴士上坐着无穷大数量的人，这些人也要入住酒店。

⬇️ 解决方法：

引入坐标的概念来识别巴士上的人。
纵列是巴士的编号，横行第一行是现有的酒店房间，横行第二行是现在已经入住的客人。
表中用巴士编号和座位号给每个新入住的客人一个唯一编号（Bus1Seat1等）。

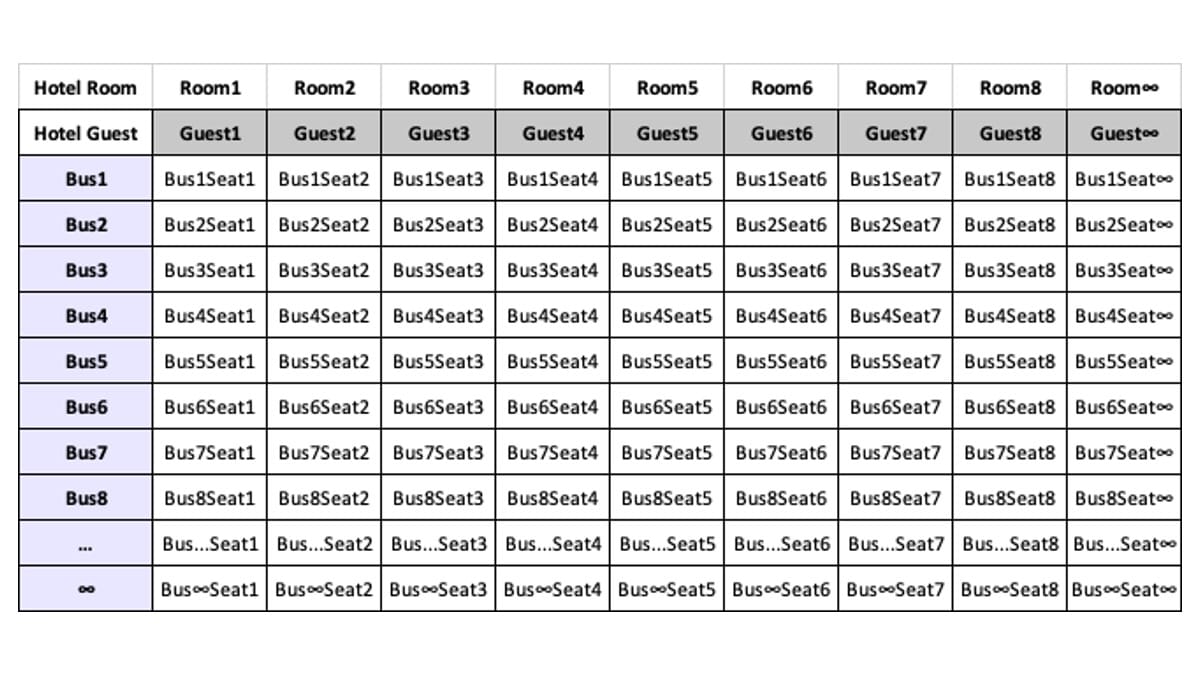
我们要做的就是将现在已经入住的客人和所有巴士上的人的编号重新排列在一行里。
视频里介绍的方法是用Z字行来画线，保证这条线经过所有编号一次且仅有一次。

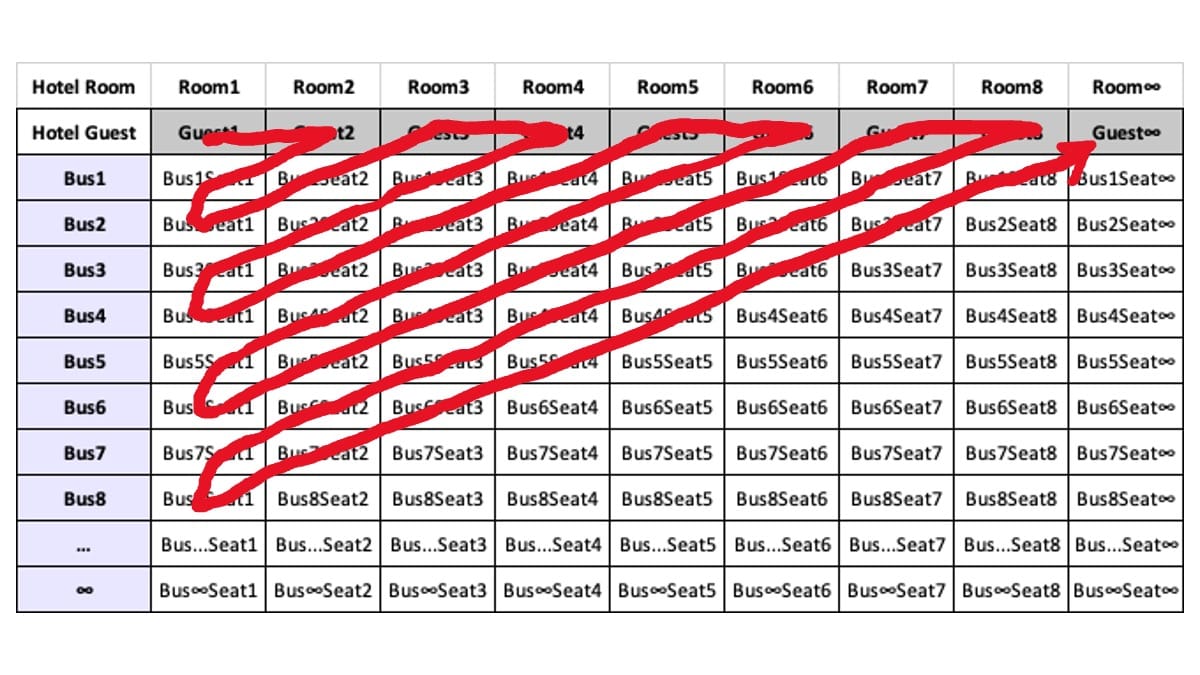
然后我们想象将这条线拉直。
于是得到排列成一行的坐标，自然的，你可以给每个编号安排一间房间。

恭喜你通关！

🕹️【第四关】

现在又来了一辆巴士。这辆巴士上没有座位。你只能靠名字识别每个个人。假设这些人的名字都是无穷大个字母A和B的唯一的排列组合。比如，有个人的名字是“ABABABBBABAABA…”，另一个人的名字是“ABBAAAAAAAAAA…”。于是这辆巴士上有字母A和B的无穷个排列组合。

⛔️ 问题出现了：

你无法保证每一个人都能有一个房间。

💡 理由：
理论上你打开Excel，使用用第三关的解决方法来安排房间。此时假设你按顺序取每个人的名字的一个字母，并反转为另一个字母，以此类推。
比如从第一个人的名字里，你将首字母的A变为B（“ABABABBBABAABA…”变为“BBABABBBABAABA…”），然后从第二个人的第二个字母从B变为A（“AABAAAAAAAAAA…”），如此往复。你永远可以保证有一个人的名字是这个组合的，无法被安排到无穷大间房间里。

这从形式上显示了有一些无穷大的集合要比另一些无穷大集合更大。